Así podemos enseñar matemáticas a través del cine

“¿Para qué me sirve a mí esto?” es una pregunta habitual que plantean los estudiantes frustrados cuando se enfrentan a la resolución de un sistema de ecuaciones o al cálculo de un máximo común divisor.
La enseñanza de las matemáticas en secundaria y bachillerato se realiza actualmente a partir de procedimientos. Sabemos, por ejemplo, cómo resolver un determinado tipo de ecuaciones, pero no para qué se aplican. Para entender la utilidad de las matemáticas, es necesario contextualizarlas.
Leer más: Por qué los problemas de matemáticas son un rollo (y cómo evitarlo)
El cine puede ser un recurso excelente en el que encontrar este tipo de contextos en los que se desarrolla un problema matemático y aprovecharlo para aprender. A veces con escenas en las que aparece descrito explícitamente un problema a resolver, y en otras ocasiones con situaciones sugeridas o imaginadas a partir de lo que vemos. Así lo explico en el libro Matemáticas a través del cine.
Jugadores de béisbol y fracciones unitarias
En la película Un entrenador de primera (Andrew Scheinman, 1994) su protagonista no sabe cómo resolver la siguiente cuestión:
“Joe y Sam tiene que pintar una casa. El primero lo hace en tres horas, mientras que el segundo necesita cinco. ¿Cuánto tardarán si la pintan juntos?”
Asistimos entonces a una colección de propuestas de solución de lo más variopinto, hasta que una persona propone utilizar una fórmula cerrada, sin mayor explicación:
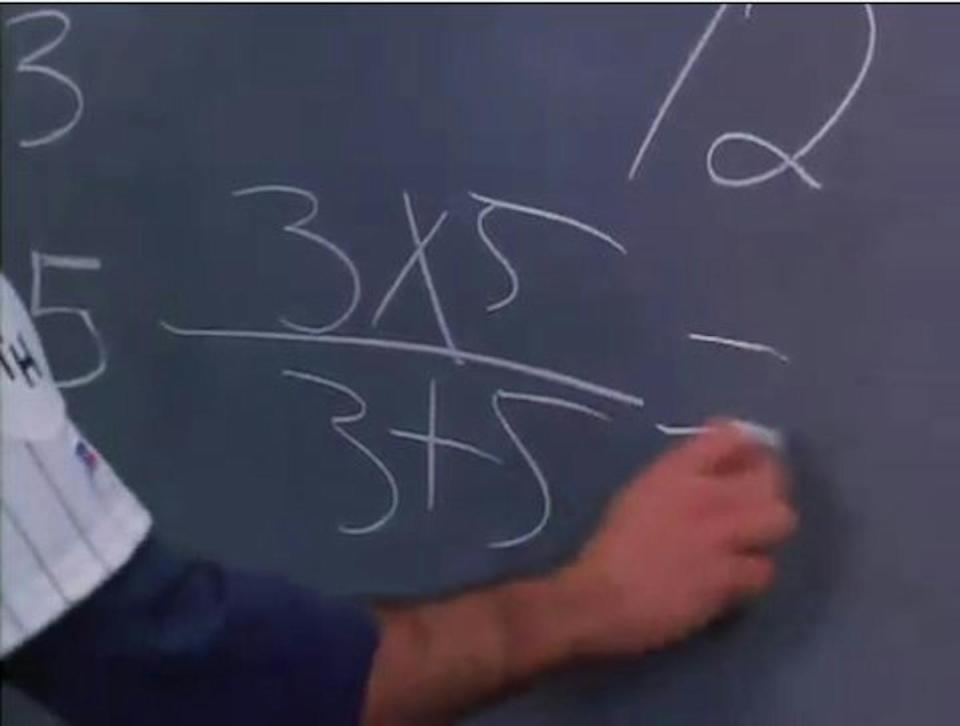
Aunque la respuesta es correcta, la memorización de expresiones matemáticas sin mayor explicación o razonamiento no es demasiado útil (¿vamos a aprender una fórmula para cada tipo de ejercicio?). Lo realmente práctico es deducir un procedimiento general.
Una posibilidad es emplear una medida común que describa el trabajo de Joe y de Sam (no 3 y 5 horas). Por ejemplo, cuánto pintaría cada uno en una hora (obviamente 1/3 y 1/5 de casa, respectivamente). Los dos juntos lo harían entonces en:
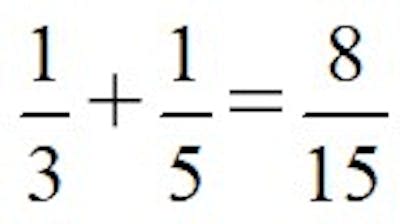
Por tanto, si 8/15 es lo que avanzan los dos en una hora, 1/(8/15) = 15/8 es el tiempo en pintar la casa completa, es decir, 1 hora y 52.5 minutos, ya que 15/8 = 1 + 7/8
Ese tipo de fracciones que se han utilizado, con numerador la unidad, se denominan “unitarias”, y fueron utilizadas por los egipcios tal y como hemos descubierto en algunos papiros. Los investigadores no conocen con certeza para qué las utilizaban, pero una utilidad que se ha encontrado es la de hacer repartos en partes iguales.
Repartos equitativos
Supongamos que hemos preparado una fiesta para la que inicialmente contábamos con 77 personas. Se encargaron 77 tartas (o pizzas, o el objeto que se deseé que pueda dividirse en trozos). Por diferentes circunstancias, al final sólo se presentan 60 invitados. Por supuesto el organizador no desea desperdiciar comida, y el sortear las tartas sobrantes no le parece justo para los que no les toque, de modo que decide que a cada uno de los 60 presentes debe corresponderle exactamente la misma cantidad de tarta. ¿Cómo deberíamos repartirlas?
Las fracciones unitarias pueden ayudarnos.
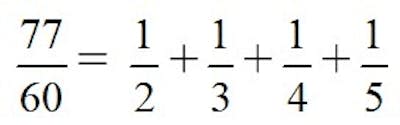
Cuando nos enseñan en la escuela a sumar fracciones, nos indican que debemos encontrar el mínimo común múltiplo de los denominadores y luego ir encontrando las fracciones equivalentes a las dadas cuando colocamos en el denominador ese mínimo común múltiplo.
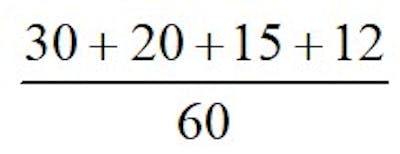
Normalmente hacemos esas operaciones mecánicamente, sin pararnos a pensar que representan. El caso es que la anterior operación nos está diciendo que 30 tartas debemos dividirlas a la mitad (véase que ½ es la fracción equivalente a 30/60), 20 en tres partes, 15 en cuatro partes y 12 en cinco partes. Dando un trozo a cada comensal de todos los obtenidos, se reparten de modo exacto e igual todas las tartas.
Quizá con un gráfico lo veamos todavía más claro:
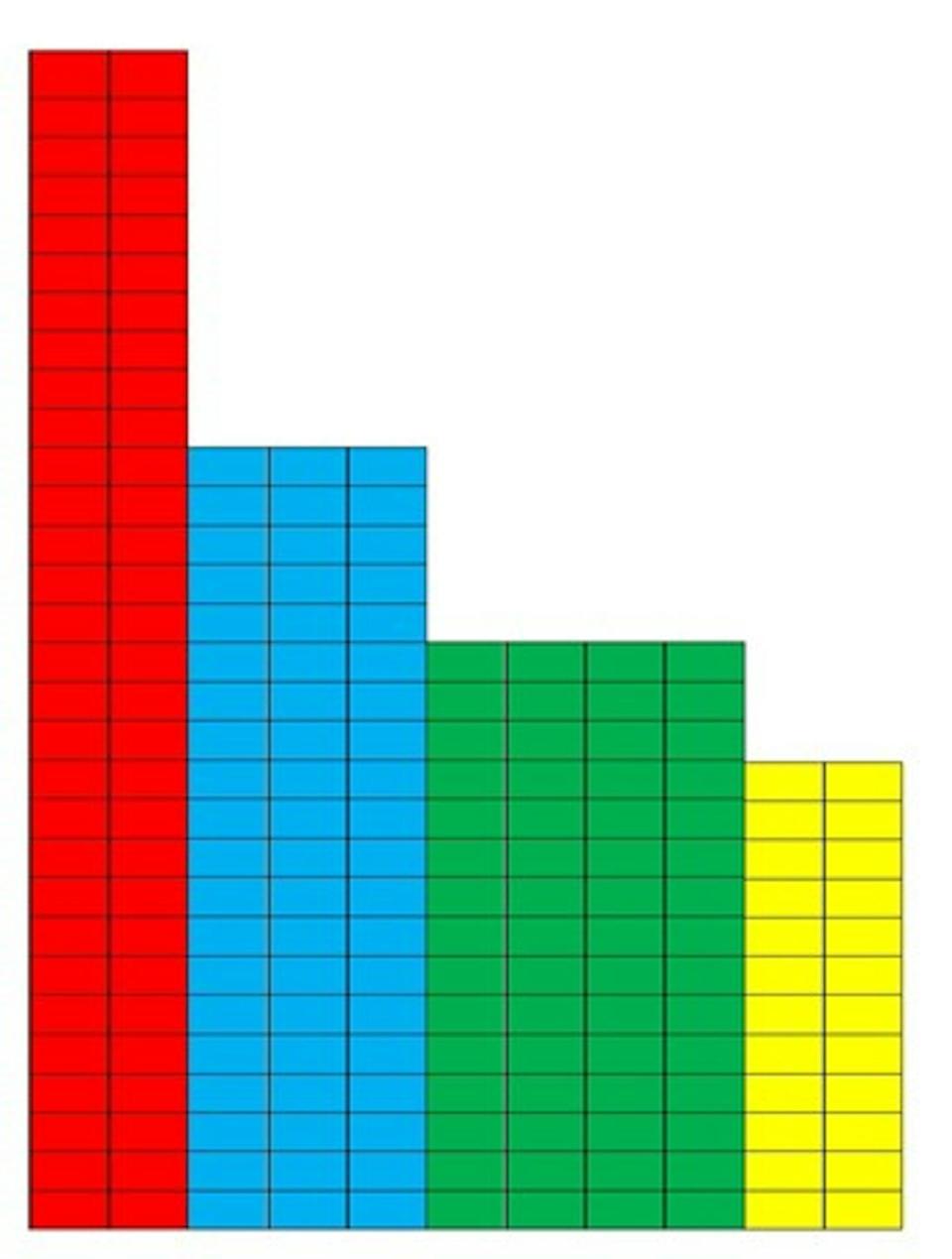
En color rojo, las 30 tartas divididas a la mitad; en azul, las 20 tartas divididas en tres trozos iguales; en verde, 15 tartas divididas en cuatro trozos iguales; en amarillo, 12 tartas divididas en cinco partes iguales. En total tenemos 240 trozos, por lo que, repartiendo un trozo de cada color a cada uno de los 60 comensales, todos tendrían la misma cantidad de tarta.
Soluciones lógicas
Sin embargo, todos hemos experimentado alguna vez que, al dividir en trozos un alimento (pizzas, por ejemplo), cuantos más cortes hagamos, más comida se desperdicia (por las migas que van formándose, además de que quizá no dispongamos de un procedimiento para hacer tres o cinco partes de manera exacta). Por tanto, sería deseable ir al procedimiento que menor número de cortes necesitara. La descomposición de una fracción en fracciones unitarias no es única. ¿Podríamos encontrar una con menos cortes?
Pensando un poco, enseguida nos percatamos de que la fracción original, 77/60 es mayor que 1. Por tanto, ¿para qué partir tantas tartas, si podemos dar alguna entera a cada invitado?
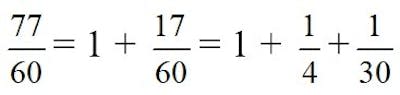
En este caso, dando a cada invitado una tarta entera y dividiendo 15 tartas en cuatro partes iguales, 2 en treinta partes iguales, también tenemos un reparto igualitario y por tanto justo. Desde luego se hacen menos trozos, pero ¿cómo dividir 2 tartas en treinta partes iguales?
Ese es otro asunto para el que quizá las matemáticas puedan servirnos de ayuda. La discusión que puede seguir a continuación es si existirá algún otro reparto “mejor”, y por supuesto llegar al “óptimo”. La descomposición en fracciones unitarias es posible sea cual sea la fracción a repartir, el planteado no es un ejemplo elegido para que quede “bonito y académico”.
John McCLane y las ecuaciones
Bruce Willis nos puede ayudar a contextualizar las ecuaciones diofánticas. En La jungla de cristal III, su personaje John McClane tiene que intentar impedir que explote una bomba antes de que termine una cuenta atrás. Para ello necesita poner 4 litros exactos en una balanza y tiene solamente la ayuda de dos garrafas, una de 5 y otra de 3 litros.
Este mismo concepto matemático lo podemos ejemplificar con un ejercicio de medida del tiempo con relojes de arena a través de una escena de La habitación de Fermat.
Y para problemas de cálculo de probabilidades, ¿qué no habrían dado los jugadores a la ruleta rusa en El cazador (1978) o los duelistas del El bueno, el feo y el malo (1968) por ser capaces de calcular sus probabilidades de supervivencia?
Entrenar el razonamiento
Si queremos demostrar que las matemáticas son útiles para la vida, el cine es un aliado a través del que encontrar esas situaciones y estimular el razonamiento: el contexto es fundamental para entrenarse en la resolución de problemas. Estas películas nos ofrecen precisamente eso, un contexto sobre el que trabajar.
Ningún ChatGPT puede de momento realizar razonamientos similares. Por ejemplo, para nuestro ejemplo anterior de las 77 pizzas y los 60 invitados, nos responde que 77 pizzas pueden dividirse en un total de 77 x 8 = 616 porciones (asumiendo que cada pizza se corta en 8 porciones iguales). Luego, para repartir equitativamente entre 60 personas, dividiríamos 616 por 60, lo que nos da aproximadamente 10.27 porciones por persona.
Y prosigue su argumento diciendo que, como no se puede repartir una fracción de una porción de pizza, se podría redondear hacia abajo o hacia arriba. En el primer caso, cada persona recibiría 10 porciones de pizza, lo que equivale a 7 pizzas para cada 60 personas. Si se redondea hacia arriba, cada persona recibiría 11 porciones de pizza, lo que equivale a 8 pizzas para cada 60 personas. Dependiendo de cuánto se quiera que reciba cada persona, hay que decidir entre estas dos opciones.
Toda una salida por la tangente, porque se dijo bien claro que queríamos partes iguales para todos. Desde luego, un escriba egipcio del siglo XVI antes de nuestra era no hubiera respondido tan rápido, pero sí mejor.
Este artículo fue publicado originalmente en The Conversation, un sitio de noticias sin fines de lucro dedicado a compartir ideas de expertos académicos.
Lee mas:
Por qué no deberíamos resignarnos a ser ‘malos’ en matemáticas
Matemáticas recreativas: ponga a prueba su destreza resolviendo enigmas históricos
Alfonso Jesús Población Sáez no recibe salario, ni ejerce labores de consultoría, ni posee acciones, ni recibe financiación de ninguna compañía u organización que pueda obtener beneficio de este artículo, y ha declarado carecer de vínculos relevantes más allá del cargo académico citado.

 Yahoo Noticias
Yahoo Noticias 
