Qué es la misteriosa ley de Zipf que encuentra patrones matemáticos en eventos azarosos

Existe un patrón sorprendente en el origen de los ganadores de la carrera de ciclismo más famosa del mundo, el Tour de Francia.
Corredores de distintos países del mundo se enfrentan entre sí durante tres semanas en una carrera que este domingo ganó el esloveno Tadej Pogacar.
Junto con miles de millones de personas, disfruto viendo el espectáculo de estos atletas casi sobrehumanos esforzándose hasta el límite absoluto en el hermoso territorio francés.
Mientras leía sobre la carrera, me encontré con un gráfico que no había visto antes: el número de victorias del Tour por nación. Lo que me llamó la atención fue el suave descenso en forma de arco de la curva de izquierda a derecha.
En particular, me di cuenta de que Bélgica, el país que ocupa el segundo lugar en términos de victorias con 18, tenía exactamente la mitad de las 36 victorias logradas por los corredores franceses. El país con el siguiente mayor número de camisetas amarillas, España, obtuvo exactamente un tercio (12) del número de victorias de Francia. Italia, la siguiente nación en la lista, obtuvo apenas una cuarta parte (10) del número de victorias francesas.
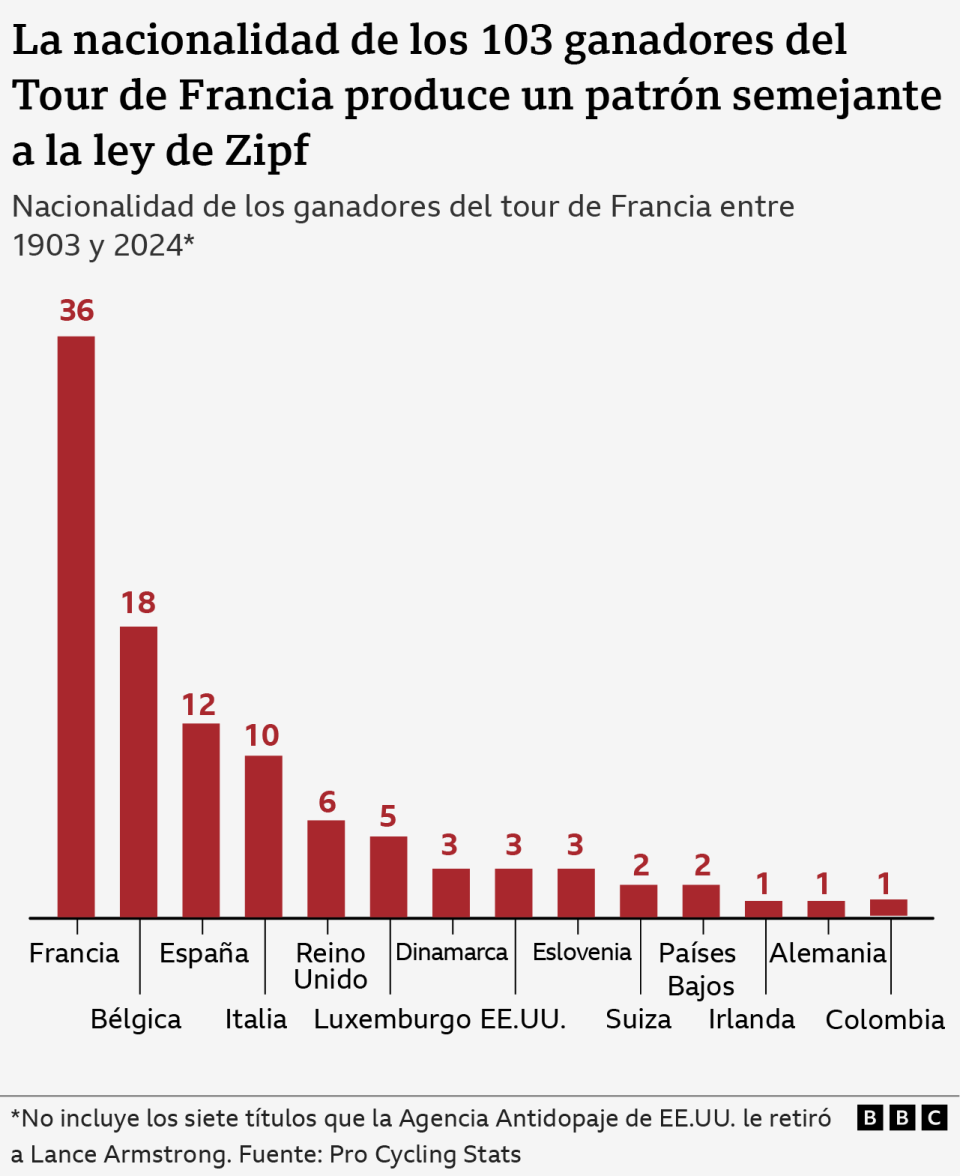
Esto me recordó mucho a una distribución misteriosa y ubicua a la que, al parecer, se ajustan muchos conjuntos de datos del mundo real. Se llama ley de Zipf y es sobre todo conocida por caracterizar la frecuencia de aparición de palabras en un texto.
La ley de Zipf en las letras
En este contexto, la ley de Zipf establece que cuando las palabras de un texto lo suficientemente extenso se alinean en orden de frecuencia decreciente, exhiben un patrón especial.
En concreto, la segunda palabra más frecuente aparece aproximadamente la mitad de veces que la número uno. La tercera palabra más frecuente aparece aproximadamente un tercio más que la primera, la cuarta una cuarta parte y así sucesivamente, tal como pasa con los ganadores del Tour de Francia.

Para ponerlo a prueba, analicé la frecuencia de palabras de uno de mis propios libros, "The Maths of Life and Death" (Las matemáticas de la vida y la muerte), y encontré una concordancia sorprendentemente buena con la ley de Zipf.
La palabra que más utilicé en el libro fue “the" (la preposición "el" o "la" en inglés) con 6.691 veces. En segundo lugar quedó "of" (la preposición "de" en inglés) con 3.330 apariciones, casi exactamente la mitad del número de veces que figura "the". La palabra "to" ("a" o "hacia") fue la siguiente con 2.445 apariciones, poco más de un tercio de la frecuencia de "the", y así sucesivamente.
Por cierto, las palabras "vida" y "matemáticas" aparecieron 64 veces, mientras que "muerte" apareció solo en 42 oportunidades, a pesar de que el título del libro era "Las matemáticas de la vida y la muerte".
Incluso al mirar los párrafos anteriores, podemos ver que hay algunas palabras extremadamente comunes, como "la" y "el", mezcladas con palabras más raras como "sorprendentemente" y "apariciones".

En un texto lo suficientemente extenso, lo que la ley de Zipf nos dice es que hay muchas más palabras raras que palabras comunes.
De hecho, la ley de Zipf sugiere que estos factores se equilibran entre sí, de modo que si extraemos una palabra al azar de un texto, es igual de probable que sea o una de las muchas palabras raras o una de las pocas comunes.
La ley de Zipf para la frecuencia de palabras en un texto extenso es universal. Es decir que no solo es válida para el inglés, sino aparentemente para muchos otros idiomas, incluyendo el esperanto, que es un idioma artificial.
Curiosamente, esta relación casi mágica no se limita a las palabras de un texto o al Tour de Francia. También ha sido reportado en escenarios extremadamente diversos, como la cantidad de artículos escritos por científicos, el tamaño de la población en asentamientos e incluso el diámetro de los cráteres de la Luna.
Ley de potencia

La ley de Zipf es un caso especial de una regla más general: la ley de potencia.
En este contexto, dichas leyes de potencia sugieren que una variable (por ejemplo, la fuerza de la atracción de la gravedad de la Tierra) varía de manera proporcionalmente inversa en relación con alguna otra variable (la distancia desde el centro de la Tierra) elevada a alguna "potencia" matemática. En el caso de la gravedad, cuanto más corta sea la distancia desde el centro de la Tierra, más fuerte será la atracción, mientras que cuanto mayor sea la distancia, más débil será la atracción.
La ley de potencia de Zipf para palabras en un texto extenso es un caso especial en el que la "potencia" o "exponente" en la ley de potencia es uno. Esto significa que duplicar una variable reduce a la mitad la otra y que triplicar la primera disminuye la segunda en un tercio y así sucesivamente.
Sin embargo, para una ley de potencia general, este no suele ser el caso. La ley del cuadrado inverso de la gravitación, por ejemplo, sigue una ley de potencia cuyo exponente (o potencia) es dos. Si te alejaras el doble del centro de la Tierra en comparación con donde estás sentado actualmente, entonces la fuerza que experimentarías en tu nueva posición sería cuatro (dos al cuadrado) veces más débil que donde estás ahora. Si te alejas tres veces más, la fuerza será nueve (tres al cuadrado) veces más débil y así sucesivamente.
Se ha descubierto que las leyes de potencia describen una amplia gama de conjuntos de datos generados naturalmente, desde la variación de la diversidad de especies según el área del hábitat hasta la frecuencia del número de tornados por día en Estados Unidos e incluso el número de artistas en función del precio medio de su obra.

Pero hay más. Al analizar datos sobre las guerras entre 1809 y 1949, Lewis Richardson descubrió que la frecuencia de los conflictos fatales variaba con respecto al número de personas muertas bajo la ley de potencia elevada a la ½. Las guerras donde murieron un millón de personas eran 10 veces menos probables que aquellas en las que murieron 10.000 personas y 100 veces menos probables que los conflictos en los que murieron 100 personas.
Quizás una de las leyes de potencia más importantes jamás descubiertas fue la publicada por Charles Richter y Beno Gutenberg en 1956, que describe cómo la frecuencia de los terremotos varía con su magnitud.
Está claro que las leyes de potencia son importantes para describir una amplia gama de fenómenos del mundo real, pero ¿por qué parecen ser tan ubicuas?
Matemáticamente se puede demostrar que las leyes de potencia surgen cuando los sistemas exhiben ya sea invariabilidad de escala o autosemejanza. Los sistemas que exhiben estas propiedades relacionadas se ven iguales (o más o menos iguales) cuando nos acercamos o alejamos a ellos.
Muchos fenómenos del mundo real, desde redes como internet hasta fenómenos físicos naturales como los copos de nieve y estructuras biológicas como los helechos, exhiben propiedades autosimilares.
Las leyes de potencia capturan matemáticamente esta propiedad autosemejante.
Combinaciones interesantes
La que podría ser la explicación más convincente para la ley de Zipf sostiene que hay variables latentes o que no han sido observadas que funcionan para mezclar múltiples componentes que, tomados por sí solos, no obedecerían dicha ley, pero que cuando se combinan, sí lo hacen.
En el contexto de la frecuencia de palabras, por ejemplo, los componentes son las diferentes partes del discurso (por ejemplo, adjetivos, conjunciones, sustantivos, preposiciones, verbos, etc.). Por ejemplo, debido a que son generales y se usan en oraciones independientemente del contexto, hay muy pocas conjunciones diferentes (por ejemplo, "y", "porque"), cada una de las cuales es relativamente común. Por el contrario, aunque existen muchos más sustantivos (por ejemplo, "discurso", "ley", etc.), cada uno de ellos se puede usar únicamente en contextos específicos que son relativamente poco comunes.
Individualmente, estos componentes no obedecen la ley de Zipf, pero cuando estas partes del discurso se mezclan con otras para formar el lenguaje, sí lo hacen.
El Tour de Francia tampoco es el único contexto deportivo en el que se cumple la ley de Zipf. Ocurre en situaciones como los medalleros olímpicos y los premios en metálico del billar.
Pero no está claro exactamente por qué la ley de Zipf se aplica a los ganadores del Tour de Francia. De hecho, como era de esperarse, cuando se traza la distribución de Zipf sobre los datos reales, la concordancia no es perfecta.
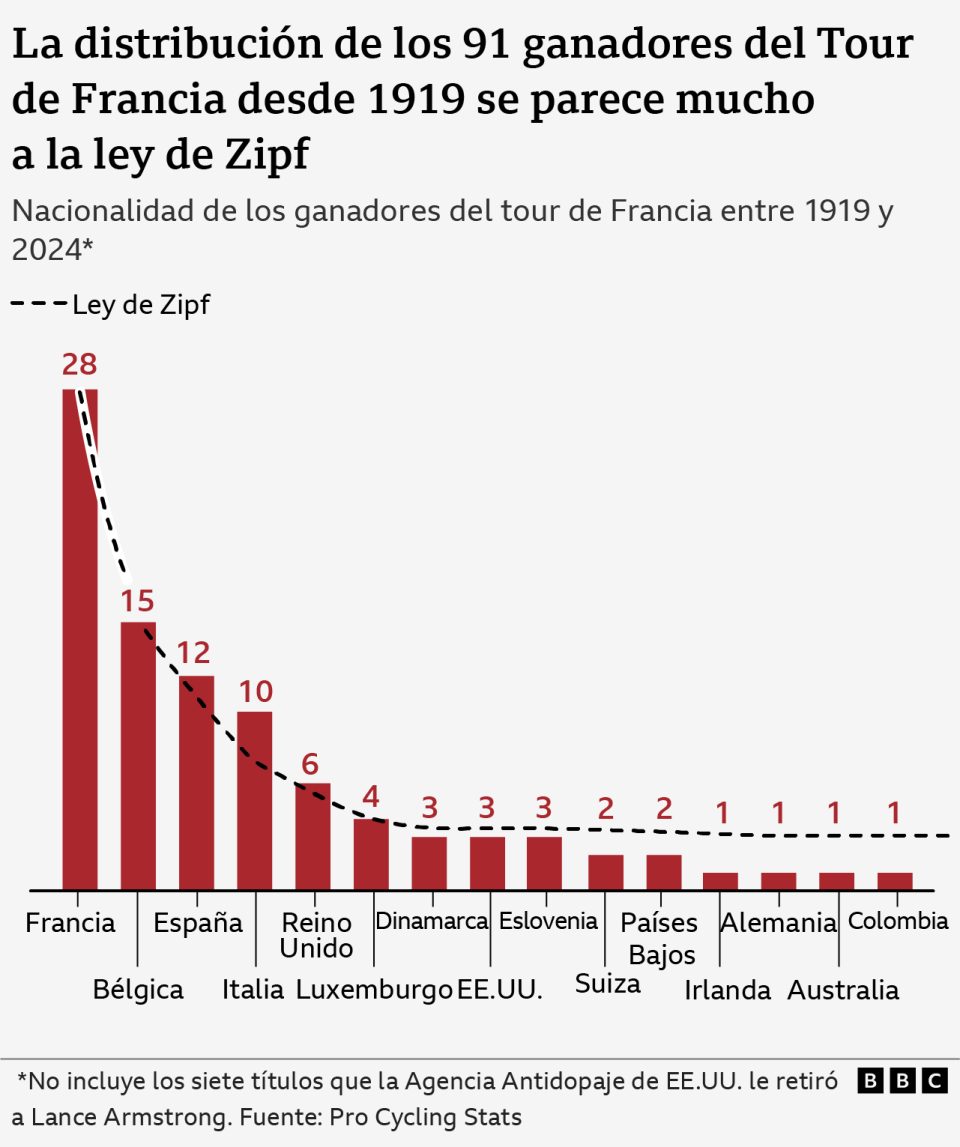
Las naciones europeas -Francia, Bélgica, España e Italia- que más han ganado el Tour, están sobrerrepresentadas. En cierto sentido esto no es sorprendente: la composición de los primeros Tours de Francia estuvo dominada por los franceses y más tarde por sus países vecinos. En la primera edición del Tour de 1903, por ejemplo, 49 de los 60 ciclistas inscritos eran franceses.
De hecho, si eliminamos a todos los ganadores antes de la Primera Guerra Mundial, podemos encontrar que la ley de Zipf concuerda mejor.
Dado que no ha habido ningún ganador francés de su evento deportivo más famoso desde 1985, algunas de las naciones subrepresentadas han tenido la oportunidad de ocupar su lugar en la distribución.
¿Pero qué significa eso para la carrera del próximo año? ¿Qué país ganará? Lamentablemente, la ley de Zipf solo habla de generalidades y no ofrece respuestas a preguntas tan específicas.
Lo seguro es que, pase lo que pase, tendrán que pasar muchos años para que la evidencia del dominio inicial del Tour por parte de Francia se desvanezca de los datos.
*Kit Yates es director del Centro de Matemática Biológica en la Universidad de Bath y autor de los libros "The Maths of Life and Death" (Las matemáticas de la vida y la muerte) y "How to Expect the Unexpected" (Cómo esperar lo inesperado).
Esta es una adaptación al español de un ensayo publicado por BBC Future. Si quieres consultarlo en su inglés original, lo puedes encontrar aquí.


 Yahoo Noticias
Yahoo Noticias 
